A study of the 24 problem

What is more annoying than those cheap attention-grabbing maths problem from social media ? They often are less brain-teasers and more specifically crafted to first, catch your eyes, with pickup lines such as 99% of people can’t solve this!!!, and then have either trick or ambiguous answers so that people fight in the comments over the correct order of operators or whether a five-petal flower is symbolically worth more than a four-petal flower in a system of emoji equations.

Sometimes, however, the problems are more interesting. And by interesting, I mean worthy of a small dive around the Catalan numbers and a few hours worth of Python programming.

In one such problem, the 24 problem, you have to use the numbers 1, 3, 4 and 6 exactly once, and any of the arithmetic operators (+,–,× and /) to make each counting number from 1 to 24. This is meant as a puzzle, and the best way I can solve this by hand is working backwards. For example. 12 is 24 divided by 2 and you can make 24 with 6 × 4 and 2 with 3 – 1 which gives.

12 = \frac{ 6 \times 4}{3 - 1}

Of course this is tiring if we are to do this twenty three more times. We can avoid the mental arithmetics and instead let the computer do the work for us by searching, among all possible combinations of numbers and operators, one that gives the desired result. Easy, right ?

Combinatorics, or the art of making lists

The problem turns into a combinatorics problem where we want to enumerate all possibilities for all orders we put the numbers, and which operators we use on them.

Figuring out all possible permutations of the given numbers, we want to try (1,3,4,6), then (1,3,6,4), then (1,4,3,6), etc. This is simple: if there are n numbers, there are n! possible permutations. We can easily list them in python with itertools

import itertools
numbers = [1,3,4,6]
for p in itertools.permutations(numbers):
     print(p)

which will correctly list all 4! = 24 possible ordering of our four numbers.

Now listing all possible choices for operators is trickier. The naive approach would assume that in between our 4 numbers we have three blank spaces to fill with 3 possible math operators, and that would be 4³= 64 different possibilities. In python, we can use itertools.combinations(operators, repeats=3) to list them all.

The problem,however, comes with parentheses. Consider :

\begin{align*}
((6 + 4) - 3) -1 &=6 \\
(6 + 4) - (3-1) &= 8
\end{align*} 

where we have picked (+, –, –), but the order of the operations changes the end result (subtraction is not associative). Since, unlike those viral facebook problems, we want to account for all possible orders of evaluation, we need to find out how to enumerate all possible way to add parentheses to the expression. So how many ways are there to unambiguously parenthesize an arithmetic expression of n operators ?

A tree for trees and for fours

A good way to think about this problem is to see an expression with parentheses as a tree. A simple expression with two numbers and an operator in between (such as 6 + 4) can be represented as a tree where the leaves are the numbers and their parent node represents the operation applied to them.

To understand how a sequence of operations in a given order is represented by a tree, let’s build one from the bottom up. To compute the result in the first equation, we first evaluate (6 + 4) = 10. The next step is to do the subtraction with 3. In tree form, we create a [–] node, and we attach as its children both the earlier [+] node at on side, and the 3 at the other, to signify that you feed the result of the addition to the subtraction with 3.

Finally we build the whole trees for the two expressions above, revealing the difference in order of evaluation:

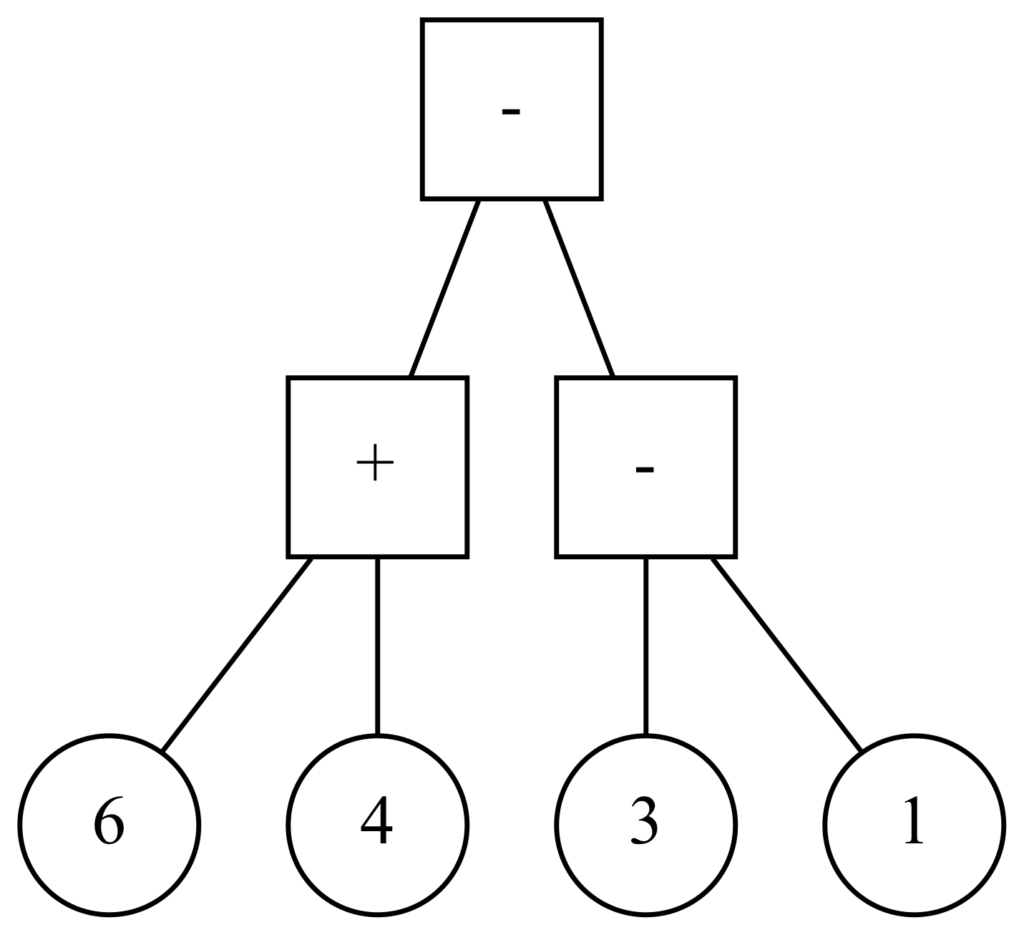
This tree of representation of the sequence of computations (or evaluations) of binary operators acting on number has a few interesting properties :

There are two types of elements of the tree: the leaves, representing the numbers, and the inner nodes, which represent an operation and have two children nodes. Those children can be either leaves or other operators. This makes the tree a full binary tree as each element has either 0 or 2 children.

In full binary trees, the number of inner nodes is equal to the number of leaves minus one. If we go back to the idea that it represents a computation for, say, four numbers, there are three “spaces” in between then to insert an operator.

At this point it is clear that there is a correspondence (more precisely a bijection) between the parentheses orderings of an expression with n operators and full binary trees with n inner nodes. We just need to find all of them.

Counting trees

How can we generate all full binary trees for a given number of operators ? We start by observing that any subtree of a full binary tree is a full binary tree, we can work our way upwards by induction (or recursion if you’re a programmer), so here we go.

Base case : there is only one full binary tree with no operator – the one with a single leaf. That wasn’t too hard.

General case : assuming we can already generate all possible full binary trees with 1, 2, 3, … n – 1 operators. We can build all full binary trees with n operators as follows. The root of our new tree is an operator node, and it must have two children (or the tree would not be full), so there is a left subtree and a right subtree, both of which are full binary trees in their own right. To cover all the cases we must therefore consider the case where the left subtree has no operator – it’s a leaf (so the right subtree has all other n – 1) , the case where the left subtree has one operator (with n – 2 in the right side), the case where it has two… and so on until n – 1 operators are in the left subtree and none in the right subtree.

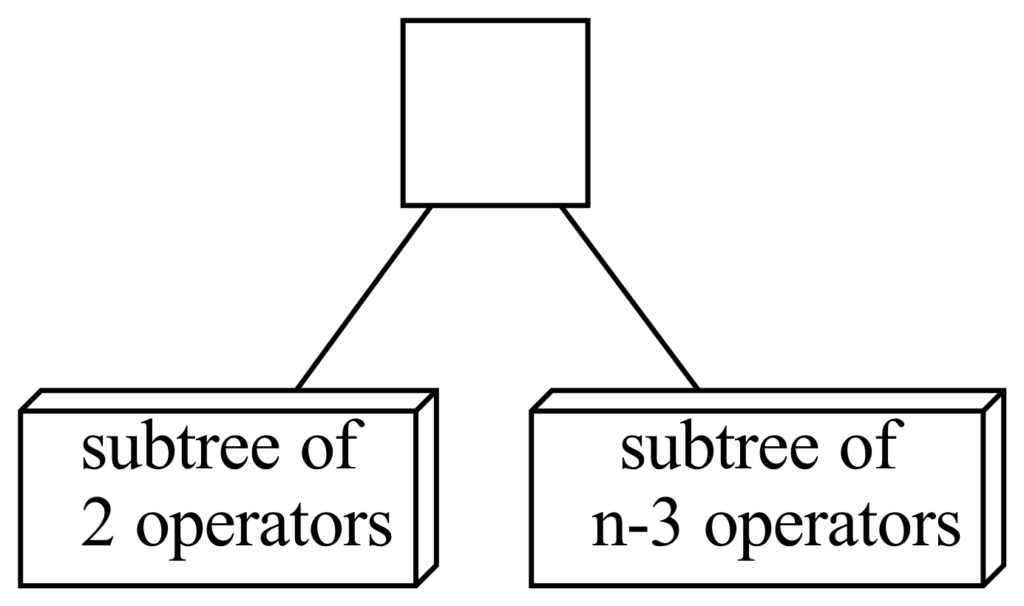
Per our hypothesis, we already know how to generate all those smaller subtrees on each side, so for each of those possible split (say, i operators to the left and n – i – 1 to the right), we need to consider of all possible left subtrees of i operators with all possible right subtrees of n – i – 1 operators.

In python, we’ll use itertools.product to list all possible choices of left and right subtrees. Using that recursive definition, we handle the base case first, and then do a loop for all splits, and a loop for the subtree combinations of smaller size which are recursively generated.

import itertools
def get_all_fbtrees(n):
    if (n == 0):
        return [()]
    list = []
    for i in range(n):
        left_subtrees = get_all_fbtrees(i)
        right_subtrees = get_all_fbtrees(n-i-1)
        for l,r in itertools.product(left_subtrees, right_subtrees):
              list.append((l,r))
    return list

Here we’re using tuples to represent the tree structure in python, with empty tuples acting as leaves. Of course in the real code, we will use an iterative version with memoization to speed up the computation, but this snippet better highlights the recursive nature of the problem.

For the 24-problem, which has four numbers and three operators, we obtain five different trees :

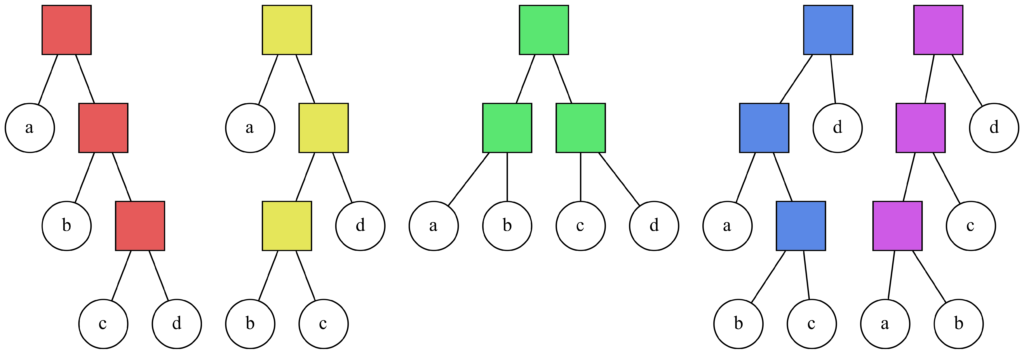
A Catalan detour

We can also derive us a recursive formula for C_n, the count of all possible full binary trees with n inner nodes (or n + 1 leaves).

\begin{align*}
C_0 &= 1\\
C_{n+1} &= \sum_{i=0}^{n} C_i \; C_{n-i}
\end{align*}

The sequence of C_n : 1, 1, 2, 5, 14, 132, 429, 1430, 4862,… the Catalan numbers, show up in so many different counting problems it’s almost no surprise to see them here. Catalan numbers, among many of their uses, also count the numbers of possible ways to triangulate polygons of n + 2 vertices. This means that for each of our expression trees, we can associate a triangulation of the pentagon.

To visualize this, let’s take a given parenthetizing of four numbers and three operators, for example ( a . ( b . ( c . d ) ) ) ), and show how we can find the associate triangulation of a pentagon. Start by labeling all edges with our numbers, leaving one empty. The ordering requires ( c . d ) to be first evaluated. That maps to making the sides c and d part of our first triangle. We write the result of the computation along the unlabelled edge of the triangle.

Next is computing b with ( c . d ), so we draw a new edge to create a new triangle with other edges b and ( c . d ), and we can fill the final edge of the polygon itself with the full expression.

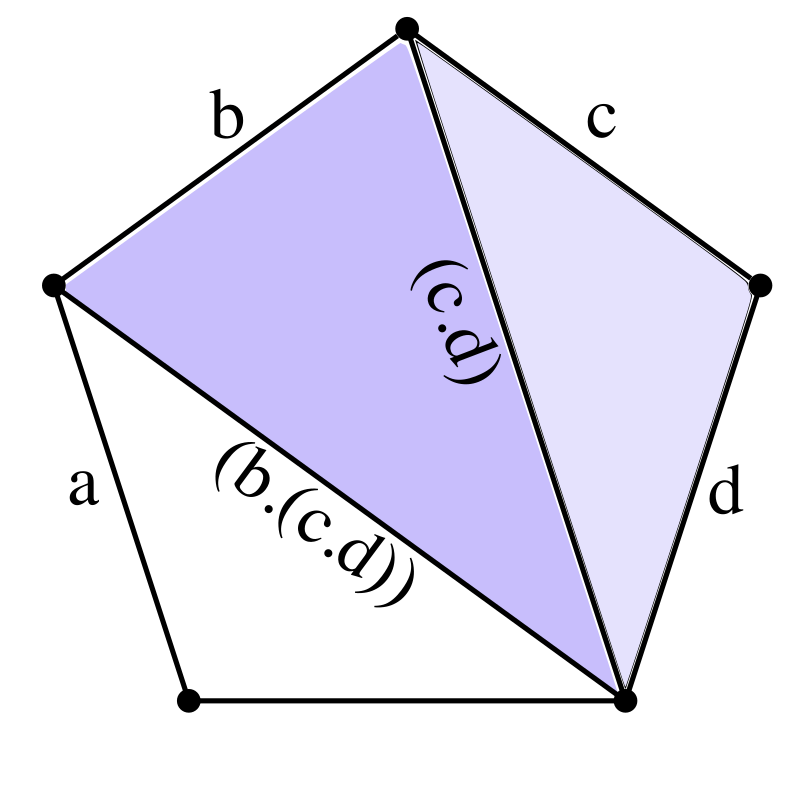
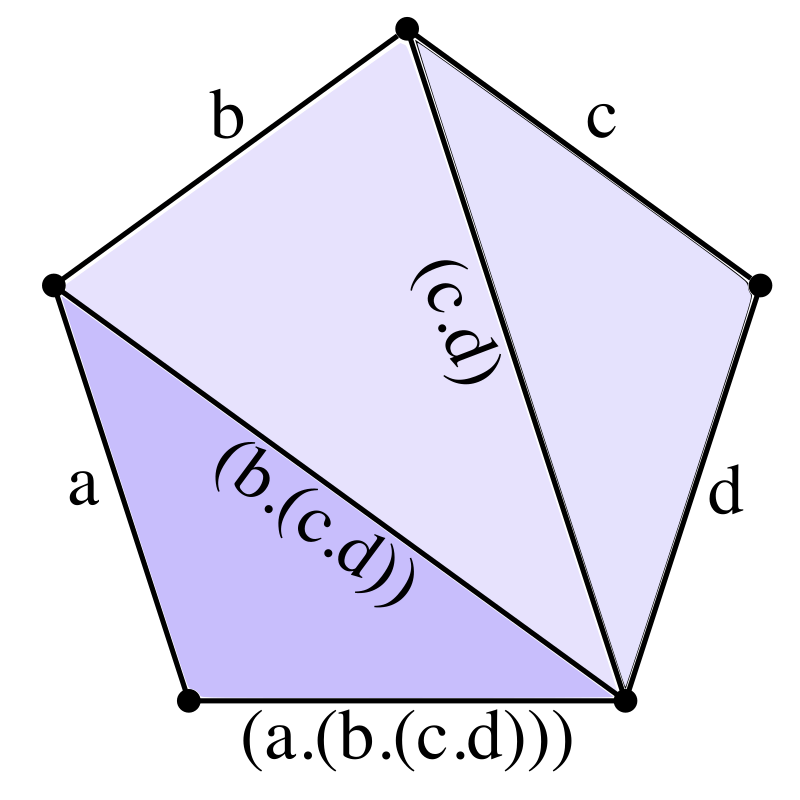
This lets us generate all possible triangulations of the pentagon, mapping to the 5 trees above :

Solving the 24 problem

After this digression, we are now ready to tackle the 24 problem. This is going to be a brute-force search :

• For all possible orderings of the numbers (6,4,3,1) – of which there are 4! = 24 total
• For all possible choice of 3 operators among (+, – , × and ÷) – of which there are 4³ = 64
• For all possible trees of evaluation – of which there are 5

This leads us to a very simple implementation (again leveraging itertools), which will go over the 24 × 64 × 5 = 7680 different possibilities and give us all the answers.

def problem_search(number_list, op_list, target):
    N = len(number_list)
    trees = get_all_fbtrees(N-1)
    found = []
    for ops,numbers in itertools.product(
            itertools.combinations(op_list,repeat=N-1),
            itertools.permutations(number_list)):

        for tree in trees:
            result = eval_tree(tree,ops,numbers)
            if (result == target):
                found.append((tree,ops,numbers))
    return found

For reference here is a list of solutions for numbers 1 to 24, with the number of found solutions. Quite interestingly, there is only one solution for 24.

\begin{align*}
((1-(3+4))+6) &= 0&\quad\footnotesize{(156)} \qquad&(4×((6×1)-3)) &= 12&\qquad\footnotesize{(150)}\\
(((3+4)×1)-6) &= 1&\quad\footnotesize{(214)} \qquad&(((6+4)+3)/1) &= 13&\qquad\footnotesize{(98)}\\
(1×((4/6)×3)) &= 2&\quad\footnotesize{(278)}\qquad&(3+(4+(1+6))) &= 14&\qquad\footnotesize{(66)}\\
((3+6)/(4-1)) &= 3&\quad\footnotesize{(64)}\qquad&((1-4)+(6×3)) &= 15&\qquad\footnotesize{(28)}\\
(((3-4)-1)+6) &= 4&\quad\footnotesize{(70)}\qquad&(4×((6+1)-3)) &= 16&\qquad\footnotesize{(22)}\\
(3+(6-(4/1))) &= 5&\quad\footnotesize{(169)}\qquad&((3×(6+1))-4) &= 17&\qquad\footnotesize{(22)}\\
((3+1)+(6-4)) &= 6&\quad\footnotesize{(353)}\qquad&(((3/1)×4)+6) &= 18&\qquad\footnotesize{(33)}\\
(((6-4)×3)+1) &= 7&\quad\footnotesize{(197)}\qquad&((3×(6-1))+4) &= 19&\qquad\footnotesize{(10)}\\
(6/((3/1)/4)) &= 8&\quad\footnotesize{(258)}\qquad&((3-1)×(4+6)) &= 20&\qquad\footnotesize{(16)}\\
((4-1)×(6-3)) &= 9&\quad\footnotesize{(41)}\qquad&((4×6)-(1×3)) &= 21&\qquad\footnotesize{(56)}\\
((6/3)×(4+1)) &= 10&\quad\footnotesize{(20)}\qquad&(4+(1×(3×6))) &= 22&\qquad\footnotesize{(52)}\\
((3×(6-1))-4) &= 11&\quad\footnotesize{(4)}\qquad&(3+(4×(6-1))) &= 23&\qquad\footnotesize{(10)}\\
&&(6/(1-(3/4))) &= 24&\qquad\footnotesize{(1)}\\
\end{align*}

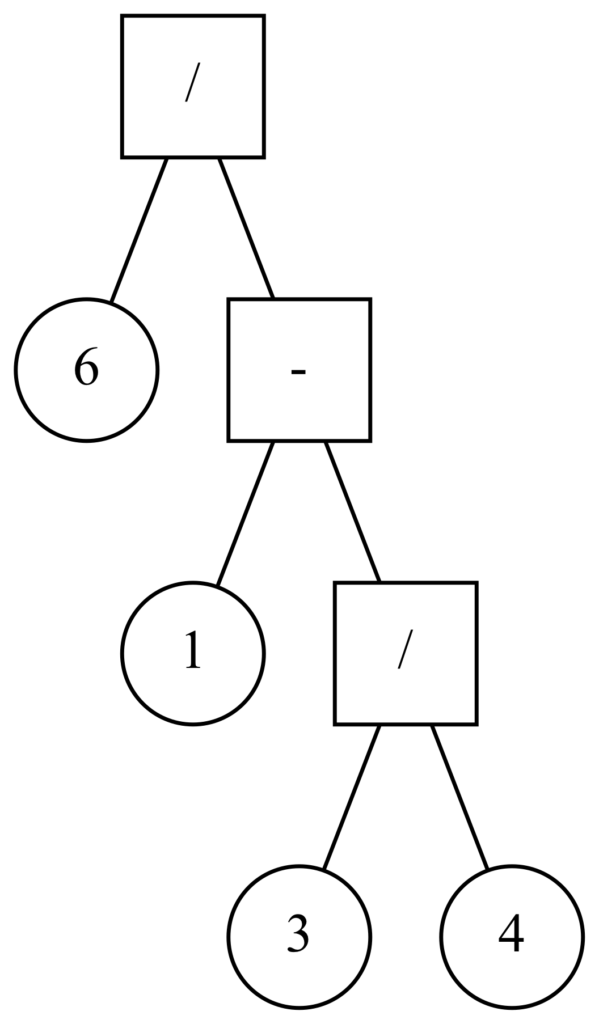
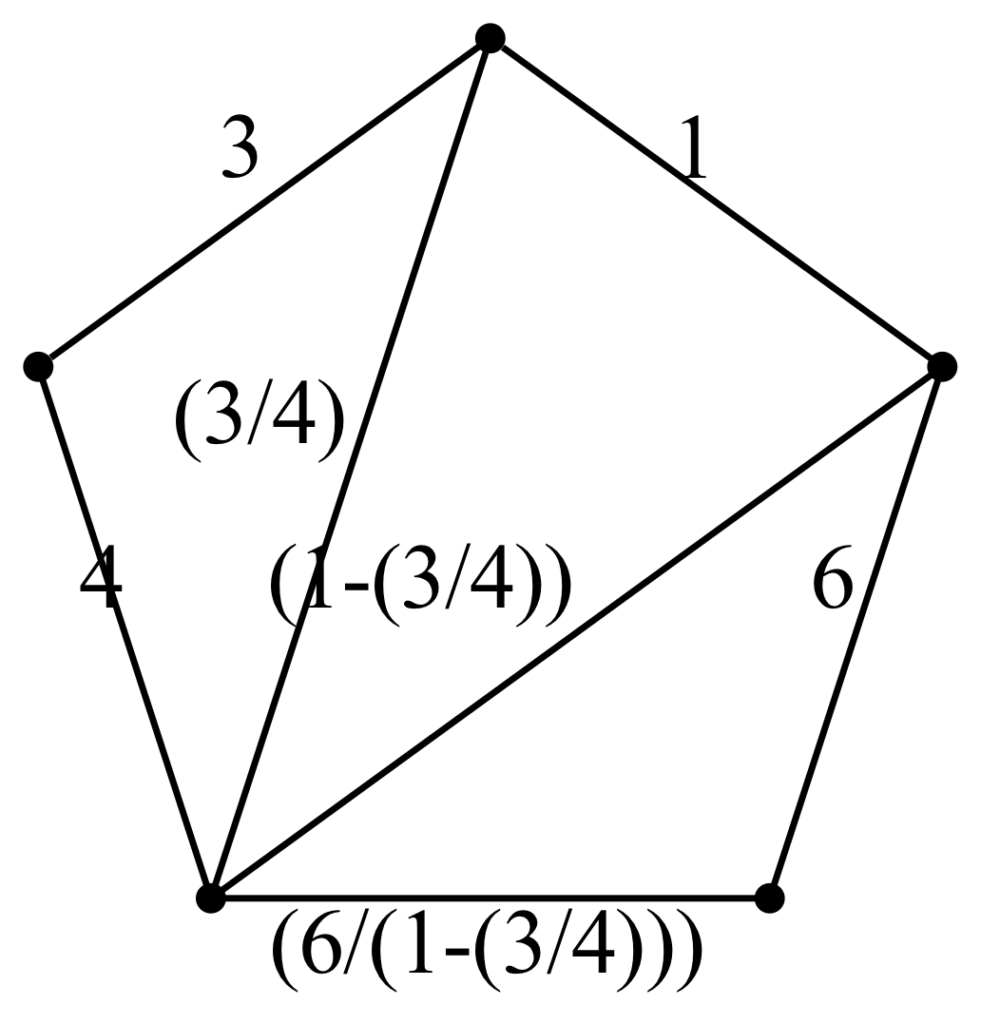
Running the code to search higher numbers, 34 is the first number for which there is no solution, at least with the 4 original arithmetic operators. And since the highest possible value is 96 = (6 × 4 × (3+1)) we can stop our search there, so here is an exhaustive list of all the numbers for which there is at least a solution :

[0 to 33, 35, 36, 37, 40, 41, 42, 43, 48, 54, 60, 66, 68, 69, 71, 72, 73, 75, 76, 78, 84, 90, 96]

Bonus graphs !

Of course there’s a lot more room for exploration ! Trying to solve similar problems like the Four fours problem would require us to examine other binary operators such as exponentiation or concatenation. The unary operators (like unary minus or factorial) would require us to augment our tree approach (each node could be decorated by one or more unary symbols !) or move to a reverse search with a hash-table memoization.

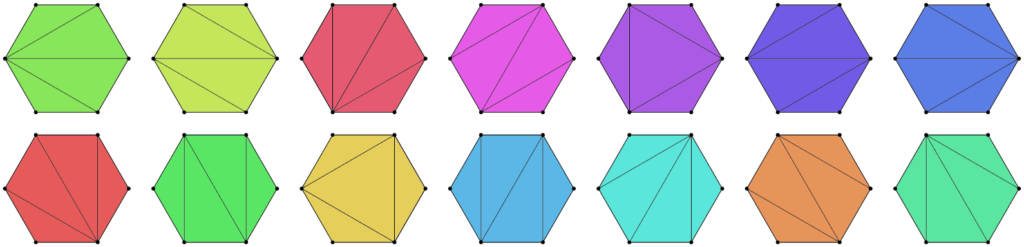
But we can also just look at bigger trees and polygons. Here’s all 14 trees with 5 leaves and all corresponding triangulated hexagons

References & Links

You can see the code (including the function to generate the graph drawings in the dot format) on my Github

• Catalan Numbers – Richard P. Stanley, 2015, Cambridge University Press
• Solving the 24-problem – Peter Collingridge, 2018
• Deux minutes pour les nombres de Catalan – El Jj, 2017
• 4444 problem – Paul Bourke