
The BBP Algorithm – π day 2021
It is pi day. Let’s have a look at a famous algorithm to compute π, the Bailey–Borwein–Plouffe (or BBP) formula which was discovered in 1995 by Simon Plouffe. Here it is in all its glory.
\pi = \sum_{k=0}^\infty \frac{1}{16^k}\left( \frac{4}{8k+1} - \frac{2}{8k+4} - \frac{1}{8k+5} - \frac{1}{8k+6} \right)Like many other π approximation formulae this one is written as an infinite series, that is, a sum of infinitely many terms, each new term getting smaller and smaller. One can compute π up to the desired precision by stopping the computation after enough terms, so it is very straightforward to implement.
double bbp_naive(uint N) {
double result = 0.0;
double div = 1.0;
for (uint k = 0; k <= N; ++k) {
const double term =
((4.0 / (k * 8 + 1))
- (2.0 / (k * 8 + 4))
- (1.0 / (k * 8 + 5))
- (1.0 / (k * 8 + 6)));
result += div * term;
printf("%d \t %.20e \t %.20e \n", k, result, result - M_PI);
div *= 1.0/16.0;
}
return result;
}This is a pretty good approximator for pi. We can check that it works by computing the first few iterations, with the correct digits highlighted
| k | value | M_PI – value |
|---|---|---|
| 0 | 3.13333333333333330373 | -8.25932025645981227058e-03 |
| 1 | 3.14142246642246636412 | -1.70187167326751875862e-04 |
| 2 | 3.14158739034658163192 | -5.26324321148408102999e-06 |
| 3 | 3.14159245756743565892 | -1.96022357457081852772e-07 |
| 4 | 3.14159264546033645260 | -8.12945666339714989590e-09 |
| 5 | 3.14159265322808778365 | -3.61705332352357800119e-10 |
| 6 | 3.14159265357288086662 | -1.69122493787199346116e-11 |
| 7 | 3.14159265358897288323 | -8.20232770593065652065e-13 |
| 8 | 3.14159265358975225979 | -4.08562073062057606876e-14 |
| 9 | 3.14159265358979133964 | -1.77635683940025046468e-15 |
| 10 | 3.14159265358979311600 | 0.00000000000000000000e+00 |
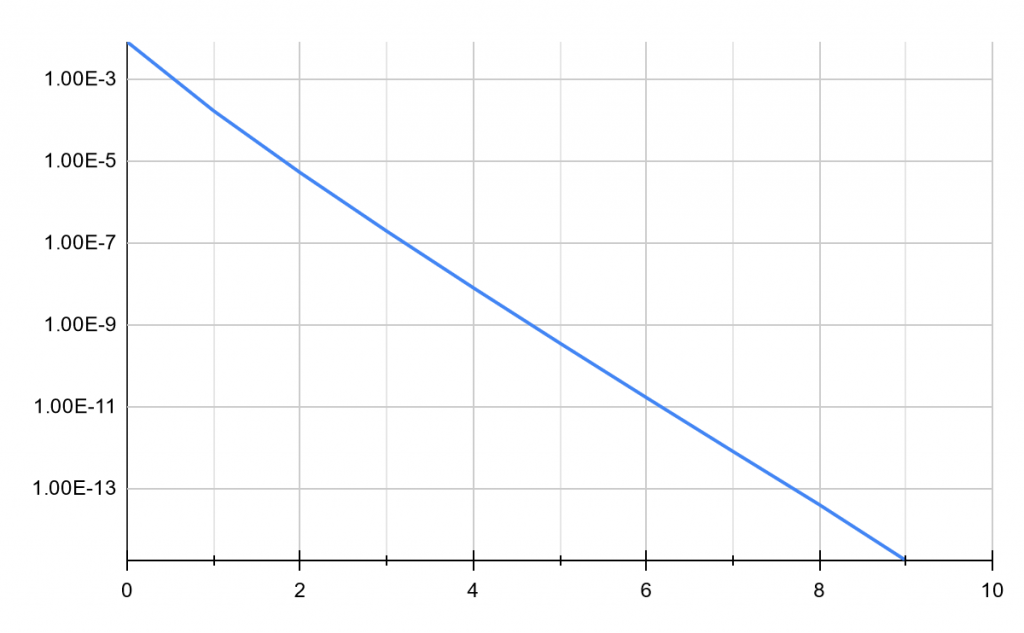
Even at k=0 the approximation (which simplifies to 47 / 15 ) is already pretty good, and at k=10 it is close enough that the difference between our approximation and the constant M_PI is rounded to zero in double precision. In fact we can see, if we plot that difference, that the formula converges exponentially fast. Nice !
However the claim to fame for the BBP formula is not only to its ability to get closer and closer to π as we increase the terms of the sum. We can use this formula to compute any digit of π, without having to compute the earlier digits. Usually, to know, say, the forty-second digit of π we would have to use a formula to compute it up to 42 significant digits. As we’ve seen, our doubles start to break down after only about 18 digits. With BBP, we can go straight to the value of digit #42 without having to compute the 0 to 41st. The limitation is that it only gives out hexadecimal digits (in base 16) and not decimal digits like we’re used to, but this should not frighten the seasoned computer scientist !
How does it work ? In base 10, to get the nth digit, you can multiply the number by 10n and look at the last digit of the integer part (its remainder modulo 10).
>>> from math import floor, pi
>>> floor(pi * 10**7) % 10)
6With a big \frac{1}{16^k} in factor for each term, the BBT formula allows for a simple expression of 16N-1 π to extract the first digit of the factional part (instead of the last of the integral part). The Wikipedia article has the full derivation, but the idea is to compute each of the four terms of the form :
\sum_{k=0}^\infty\frac{16^{n-k}}{8k + C}with (C = 1, 4,5, and 6 respectively) and then to split the infinite sum at n :
\sum_{k=0}^\infty\frac{16^{n-k}}{8k + C} = \sum_{k=0}^n\frac{16^{n-k}}{8k + C} + \sum_{k=n+1}^\infty\frac{16^{n-k}}{8k + C}In the left term, 16n-k can grow to very high values as n increases, but since we’re only interested on the first fractional digit of the overall result it’s enough to compute the modular exponential (i.e. 16n-k mod 8k + C) to get the correct decimal places without the risk of the computation blowing up.
On the right part, we still have an infinite sum to deal with. But as k grows 16n-k will rapidly vanish. Again, since only the first fractional digit matters, we can only add a few terms before they will stop affecting the final result.
template <uint C>
float bbp_sum(uint n) {
// Multiply by 16 ^ n-1 to get the nth digit
// Including digit 0 = 3 etc.
// finite sum [0.. n]
float left = 0.f;
for (uint k = 0; k < n; ++k) {
const uint den = 8*k + C;
const uint num = modular_exp(16, n-1-k, den);
left += (float(num) / float(den));
}
// partial infinite sum [ n+1 .. ] for five terms
const uint extra_iters = 5;
float div = 16.0;
float right = 0.f;
for (uint k = n ; k < n + extra_iters; ++k) {
const uint den = 8*k + C;
right += 1.f / (div * den);
div *= 16.0;
}
return left+right;
}The only thing left is to combine all four parts of the original formula with 4 values of C and “extract” the first digit we’re interested in, by forcing a 1 in the integral part, multiplying by 16 and rounding down to the nearest integer.
const float bbp_result =
4.f * bbp_sum<1>(n)
- 2.f * bbp_sum<4>(n)
- bbp_sum<5>(n)
- bbp_sum<6>(n);
// extract nth digit
const float scaled_result = bbp_result - (int)(bbp_result) + 1.f;
return (uint)( 16.f * (scaled_result - (int)(scaled_result)));You can now have the first 1000 hexadecimal digits of pi in the blink of an eye:
3.243f6a8885a308d313198a2e03707344a4093822299f31d0082efa98ec4e6c89452821e638d01377be5466cf34e90c6cc0ac29b7c97c50dd3f84d5b5b54709179216d5d98979fb1bd1310ba698dfb5ac2ffd72dbd01adfb7b8e1afed6a267e96ba7c9045f12c7f9924a19947b3916cf70801f2e2858efc16636920d871574e69a458fea3f4933d7e0d95748f728eb658718bcd5882154aee7b54a41dc25a59b59c30d5392af26013c5d1b023286085f0ca417918b8db38ef8e79dcb0603a180e6c9e0e8bb01e8a3ed71577c1bd314b2778af2fda55605c60e65525f3aa55ab945748986263e8144055ca396a2aab10b6b4cc5c341141e8cea15486af7c72e993b3ee1411636fbc2a2ba9c55d741831f6ce5c3e169b87931eafd6ba336c24cf5c7a325381289586773b8f48986b4bb9afc4bfe81b6628219361d809ccfb21a991487cac605dec8032ef845d5de98575b1dc262302eb651b8823893e81d396acc50f6d7ff383f442392e0b4482a484200469c8f04a9e1f9b5e21c66842f6e96c9a670c9c61abd388f06a51a0d2d8542f68960fa728ab5133a36eef0b6c137a3be4ba3bf0507efb2a98a1f1651d39af017666ca593e82430e888cee8619456f9fb47d84a5c33b8b5ebee07f75d885c12073301a449f56c16aa64ed3aa62363f77061bfedf72429b023d37d0d724d00a1248db1fead3Now the performance of this algorithm tends to be bound by the modular exponentiation : operation which is linearithmic O (n log n), so computing all digits up to n will be somewhere in O(n2 log n). The good news is that the computation can be heavily parallelized, this might be a good candidate for a GPU implementation !
Check out the code on https://github.com/louen/bbp. Happy pi day !
